Clasificación de funciones
CLASIFICACIÓN DE LAS FUNCIONES
- Por su composición y estructura matemática: ( Funciones algebraicas)
- Por su dominio, recorrido y regla de correspondencia (Funciones inyectivas, sobreyectivas y biyectivas)
- Por su comportamiento gráfico, ya sea general o local ( continuas, discontinuas, crecientes y decrecientes.)
FUNCIONES ALGEBRAICAS
Las funciones algebraicas se caracterizan porque en su estructura matemática solo aparecen las operaciones: suma, resta, multiplicación y división. elevar a las potencias enteras y la extracción de raíces de cualquier indice natural.
Según las operaciones que hayan sido empleadas en su composición, las funciones algebraicas se dividen a su vez en polinomiales, racionales y radicales.
En matemáticas, una función algebraica es una función que satisface una ecuación polinómica cuyos coeficientes son a su vez polinomios o monomios. Por ejemplo, una función algebraica de una variable x es una solución y a la ecuación
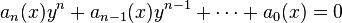
donde los coeficientes ai(x) son funciones polinómicas de x. Una función que no es algebraica es denominada una función trascendente.
FUNCIONES POLINOMIALES
Recordemos que en un monomio en una variable es la estructura algebraica formada por una constante que multiplica a dicha variable elevada a una potencia entera mayor o igual que cero.
Llamaos Polinomio la estructura formada por la suma de dos o mas monomios.
Decimos que f(x) es una Función Polinomial cuando en la composición de su regla de correspondencia solo figuran las operaciones suma, resta y multiplicación.
Las funciones polinomiales están entre las expresiones mas sencillas del álgebra. Es fácil evaluarlas, solo requieren sumas multiplicaciones repetidas. Debido a esto, con frecuencia se usan para aproximar otras funciones mas complicadas. Una función polinomial es una función cuya regla esta dada por un polinomio en una variable. El grado de una función polinomial es el grado del polinomio en una variable, es decir, la potencia mas alta que aparece de x.
Definición Si una función f está definida por
f(x) = anXn + an1 − 1Xn − 1 + an − 2Xn − 2 + ... + a1 + a0 donde a0,a1,...,an son números reales 
y n es un entero no negativo.
Entonces, f se llama una Función Polinomial de grado n.
CLASIFICACIÓN DE LAS FUNCIONES
- Por su composición y estructura matemática: ( Funciones algebraicas)
- Por su dominio, recorrido y regla de correspondencia (Funciones inyectivas, sobreyectivas y biyectivas)
- Por su comportamiento gráfico, ya sea general o local ( continuas, discontinuas, crecientes y decrecientes.)
FUNCIONES ALGEBRAICAS
Las funciones algebraicas se caracterizan porque en su estructura matemática solo aparecen las operaciones: suma, resta, multiplicación y división. elevar a las potencias enteras y la extracción de raíces de cualquier indice natural.
Según las operaciones que hayan sido empleadas en su composición, las funciones algebraicas se dividen a su vez en polinomiales, racionales y radicales.
En matemáticas, una función algebraica es una función que satisface una ecuación polinómica cuyos coeficientes son a su vez polinomios o monomios. Por ejemplo, una función algebraica de una variable x es una solución y a la ecuación
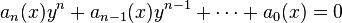
donde los coeficientes ai(x) son funciones polinómicas de x. Una función que no es algebraica es denominada una función trascendente.
FUNCIONES POLINOMIALES
Recordemos que en un monomio en una variable es la estructura algebraica formada por una constante que multiplica a dicha variable elevada a una potencia entera mayor o igual que cero.
Llamaos Polinomio la estructura formada por la suma de dos o mas monomios.
Decimos que f(x) es una Función Polinomial cuando en la composición de su regla de correspondencia solo figuran las operaciones suma, resta y multiplicación.
Las funciones polinomiales están entre las expresiones mas sencillas del álgebra. Es fácil evaluarlas, solo requieren sumas multiplicaciones repetidas. Debido a esto, con frecuencia se usan para aproximar otras funciones mas complicadas. Una función polinomial es una función cuya regla esta dada por un polinomio en una variable. El grado de una función polinomial es el grado del polinomio en una variable, es decir, la potencia mas alta que aparece de x.
Definición Si una función f está definida por f(x) = anXn + an1 − 1Xn − 1 + an − 2Xn − 2 + ... + a1 + a0 donde a0,a1,...,an son números reales
Ejemplo #1
f(x) = 3x5 − x2 + 7x − 1 es una función polinomial de grado 5.
f(x) = 3x5 − x2 + 7x − 1 es una función polinomial de grado 5.
Función Lineal
Una función lineal es una función polinomial de grado 1.
f(x) = ax + b
Una función lineal es una función polinomial de grado 1.
Función Cuadratica
Si el grado de una función polinomial es 2, se llama Función Cuadrática.
f(x) = ax2 + bx + c
Si el grado de una función polinomial es 2, se llama Función Cuadrática.
Función Racional
Una función que puede expresarse como el cociente de dos funciones polinomiales
Q(x) = f(x) / g(x)
se llama función racional.
Una función que puede expresarse como el cociente de dos funciones polinomiales
se llama función racional.
Función Algebraica
Una función algebraica es aquella que está formada por un número finito de operaciones algebraicas sobre la función identidad y la función constante.
Una función algebraica es aquella que está formada por un número finito de operaciones algebraicas sobre la función identidad y la función constante.
Funciones Trascendentes
Las funciones trascendentes son las trigonométricas, exponenciales y logarítmicas.
GRÁFICAS DE FUNCIONES POLINOMIALES GRADOS 0,1 Y 2
GRADO CERO: se llaman funciones constantes, pues es el valor de y f(x) siempre es constante (c=a) .Sus gráficas siempre son rectas horizontales.
GRADO UNO : Se llaman funciones lineales. Sus gráficas son rectas y=mx*+b, donde m = aº es la pendiente y b= aº es la ordenada en el origen.
GRADO DOS: f(x) ax2+bx+c . Conocidas como funciones cudraticas. Sus Gráficas son parábolas.
Las funciones trascendentes son las trigonométricas, exponenciales y logarítmicas.
GRÁFICAS DE FUNCIONES POLINOMIALES GRADOS 0,1 Y 2
GRADO CERO: se llaman funciones constantes, pues es el valor de y f(x) siempre es constante (c=a) .Sus gráficas siempre son rectas horizontales.
GRADO UNO : Se llaman funciones lineales. Sus gráficas son rectas y=mx*+b, donde m = aº es la pendiente y b= aº es la ordenada en el origen.
GRADO DOS: f(x) ax2+bx+c . Conocidas como funciones cudraticas. Sus Gráficas son parábolas.
Funciones algebraicas
En las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción, multiplicación, división, potenciación y radicación.
Las funciones algebraicas pueden ser:
En las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción, multiplicación, división, potenciación y radicación.
Las funciones algebraicas pueden ser:
Funciones explícitas
En las funciones explícitas se pueden obtener las imágenes de x por simple sustitución.
f(x) = 5x - 2
En las funciones explícitas se pueden obtener las imágenes de x por simple sustitución.
f(x) = 5x - 2
Funciones implícitas
En las funciones implícitas no se pueden obtener las imágenes de x por simple sustitución, sino que es preciso efectuar operaciones.
5x - y - 2 = 0
En las funciones implícitas no se pueden obtener las imágenes de x por simple sustitución, sino que es preciso efectuar operaciones.
5x - y - 2 = 0
Funciones polinómicas
Las funciones polinómicas vienen definidas por un polinomio.
f(x) = a0 + a1 x + a1 x² + a1 x³ +··· + an xn
Su dominio es 
, es decir, cualquier número real tiene imagen.
Las funciones polinómicas vienen definidas por un polinomio.
f(x) = a0 + a1 x + a1 x² + a1 x³ +··· + an xn
Su dominio es , es decir, cualquier número real tiene imagen.
, es decir, cualquier número real tiene imagen.Funciones constantes
El criterio viene dado por un número real.
f(x)= k
La gráfica es una recta horizontal paralela a al eje de abscisas.
El criterio viene dado por un número real.
f(x)= k
La gráfica es una recta horizontal paralela a al eje de abscisas.
Funciones polinómica de primer grado
f(x) = mx +n
Su gráfica es una recta oblicua, que queda definida por dos puntos de la función.
La función afín es del tipo:
y = mx + n
m es la pendiente de la recta.
La pendiente es la inclinación de la recta con respecto al eje de abscisas.
Dos rectas paralelas tienen la mismapendiente.
La función lineal es del tipo:
y = mx
Su gráfica es una línea recta que pasa por el origen de coordenadas.
y = 2x
x 0 1 2 3 4 y = 2x 0 2 4 6 8
f(x) = mx +n
Su gráfica es una recta oblicua, que queda definida por dos puntos de la función.
La función afín es del tipo:
y = mx + n
m es la pendiente de la recta.
La pendiente es la inclinación de la recta con respecto al eje de abscisas.
Dos rectas paralelas tienen la mismapendiente.
La función lineal es del tipo:
y = mx
Su gráfica es una línea recta que pasa por el origen de coordenadas.
y = 2x
| x | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| y = 2x | 0 | 2 | 4 | 6 | 8 |
Pendiente
m es la pendiente de la recta.
La pendiente es la inclinación de la recta con respecto al eje de abscisas.
Si m > 0 la función es creciente y ángulo que forma la recta con la parte positiva del eje OX es agudo.
Si m < 0 la función es decreciente y ángulo que forma la recta con la parte positiva del eje OX es obtuso.
La función identidad es del tipo:
f(x) = x
Su gráfica es la bisectriz del primer y tercer cuadrante.
Por tanto la recta forma con la parte positiva del eje de abscisas un ángulo de 45º y tiene de pendiente: m = 1.
m es la pendiente de la recta.
La pendiente es la inclinación de la recta con respecto al eje de abscisas.
Si m > 0 la función es creciente y ángulo que forma la recta con la parte positiva del eje OX es agudo.
Si m < 0 la función es decreciente y ángulo que forma la recta con la parte positiva del eje OX es obtuso.
La función identidad es del tipo:
f(x) = x
Su gráfica es la bisectriz del primer y tercer cuadrante.
Por tanto la recta forma con la parte positiva del eje de abscisas un ángulo de 45º y tiene de pendiente: m = 1.
Funciones cuadráticas
f(x) = ax² + bx +c
Son funciones polinómicas es de segundo grado, siendo su gráfica una parábola.
f(x) = ax² + bx +c
Son funciones polinómicas es de segundo grado, siendo su gráfica una parábola.
Funciones a trozos
Son funciones definidas por distintos criterios, según los intervalos que se consideren.
Las funciones en valor absoluto se transforman en funciones a trozos, siguiendo los siguientes pasos:
1. Se iguala a cero la función, sin el valor absoluto, y se calculan sus raíces.
2. Se forman intervalos con las raíces y se evalúa el signo de cada intervalo.
3. Definimos la función a trozos, teniendo en cuenta que en los intervalos donde la x es negativa se cambia el signo de la función.
4 Representamos la función resultante.
La función parte entera de x hace corresponder a cada número real el número entero inmediatamente inferior.
f(x) = E (x)
x 0 0.5 0.9 1 1.5 1.9 2 f(x) = E(x) 0 0 0 1 1 1 2
f(x) = x - E (x)
x 0 0.5 0.9 1 1.5 1.9 2 f(x) = x - E(x) 0 0.5 0.9 0 0.5 0.9 0
f(x) = x + 1 − E(x)
x 0 0.5 0.9 1 1.5 1.9 2 f(x) = x + 1 - E(x) 1 1.5 1.9 1 1.5 1.9 1
f(x) = 2x − E(x)
x 0 0.5 0.9 1 1.5 1.9 2 E(x) 0 1.5 1.9 1 2 2.7 3
La función mantisa hace corresponder a cada número el mismo número menos su parte entera.
f(x) = x - E (x)
x 0 0.5 0.9 1 1.5 1.9 2 f(x) = x - E(x) 0 0.5 0.9 0 0.5 0.9 0
f(x) = sgn(x)
Son funciones definidas por distintos criterios, según los intervalos que se consideren.
Las funciones en valor absoluto se transforman en funciones a trozos, siguiendo los siguientes pasos:
1. Se iguala a cero la función, sin el valor absoluto, y se calculan sus raíces.
2. Se forman intervalos con las raíces y se evalúa el signo de cada intervalo.
3. Definimos la función a trozos, teniendo en cuenta que en los intervalos donde la x es negativa se cambia el signo de la función.
4 Representamos la función resultante.
La función parte entera de x hace corresponder a cada número real el número entero inmediatamente inferior.
f(x) = E (x)
| x | 0 | 0.5 | 0.9 | 1 | 1.5 | 1.9 | 2 |
|---|---|---|---|---|---|---|---|
| f(x) = E(x) | 0 | 0 | 0 | 1 | 1 | 1 | 2 |
f(x) = x - E (x)
| x | 0 | 0.5 | 0.9 | 1 | 1.5 | 1.9 | 2 |
|---|---|---|---|---|---|---|---|
| f(x) = x - E(x) | 0 | 0.5 | 0.9 | 0 | 0.5 | 0.9 | 0 |
f(x) = x + 1 − E(x)
| x | 0 | 0.5 | 0.9 | 1 | 1.5 | 1.9 | 2 |
|---|---|---|---|---|---|---|---|
| f(x) = x + 1 - E(x) | 1 | 1.5 | 1.9 | 1 | 1.5 | 1.9 | 1 |
f(x) = 2x − E(x)
| x | 0 | 0.5 | 0.9 | 1 | 1.5 | 1.9 | 2 |
|---|---|---|---|---|---|---|---|
| E(x) | 0 | 1.5 | 1.9 | 1 | 2 | 2.7 | 3 |
La función mantisa hace corresponder a cada número el mismo número menos su parte entera.
f(x) = x - E (x)
| x | 0 | 0.5 | 0.9 | 1 | 1.5 | 1.9 | 2 |
|---|---|---|---|---|---|---|---|
| f(x) = x - E(x) | 0 | 0.5 | 0.9 | 0 | 0.5 | 0.9 | 0 |
f(x) = sgn(x)
Funciones racionales
El criterio viene dado por un cociente entre polinomio:
El dominio lo forman todos los números reales excepto los valores de x que anulan el denominador.
El criterio viene dado por un cociente entre polinomio:
El dominio lo forman todos los números reales excepto los valores de x que anulan el denominador.
Funciones radicales
El criterio viene dado por la variable x bajo el signo radical.
El dominio de una función irracional de índice impar es R.
El dominio de una función irracional de índice par está formado por todos los valores que hacen que el radicando sea mayor o igual que cero.
El criterio viene dado por la variable x bajo el signo radical.
El dominio de una función irracional de índice impar es R.
El dominio de una función irracional de índice par está formado por todos los valores que hacen que el radicando sea mayor o igual que cero.
Funciones trascendentes
En las funciones trascendentes la variable independiente figura como exponente, o como índice de la raíz, o se halla afectada del signo logaritmo o de cualquiera de los signos que emplea la trigonometría.
En las funciones trascendentes la variable independiente figura como exponente, o como índice de la raíz, o se halla afectada del signo logaritmo o de cualquiera de los signos que emplea la trigonometría.
Función exponencial
Sea a un número real positivo. La función que a cada número real x le hace corresponder la potencia ax se llama función exponencial de base a y exponente x.
Sea a un número real positivo. La función que a cada número real x le hace corresponder la potencia ax se llama función exponencial de base a y exponente x.
Funciones logarítmicas
La función logarítmica en base a es la función inversa de la exponencial en base a.
La función logarítmica en base a es la función inversa de la exponencial en base a.
Funciones trigonométricas
La funciones trigonométricas asocian a cada número real, x, el valor de la razón trigonométrica del ángulo cuya medida en radianes es x.
La funciones trigonométricas asocian a cada número real, x, el valor de la razón trigonométrica del ángulo cuya medida en radianes es x.
Función seno
f(x) = sen x
f(x) = sen x
Función coseno
f(x) = cosen x
f(x) = cosen x
Función tangente
f(x) = tg x
f(x) = tg x
Función cosecante
f(x) = cosec x
f(x) = cosec x
Función secante
f(x) = sec x
f(x) = sec x
Función cotangente
f(x) = cotg x
f(x) = cotg x
No hay comentarios:
Publicar un comentario